LIO-SAM 논문 리뷰 (적는 중)

배경

LiDAR-inertial SLAM을 논할 때 항상 나오는 LIO-SAM 논문을 리뷰합니다.

LiDAR-inertial SLAM은 LiDAR 센서와 IMU 센서를 함께 사용해 로봇의 자세와 지도를 실시간으로 추정하는 기술입니다.

1저자인 Tixiao Shan은 이전 2018년도 Lego-Loam의 저자이기도 합니다.

 

Abstract

• LIO-SAM은 smoothing and mapping 기법을 사용해 구현한 tightly-coupled LiDAR inertial odometry이다.
  • LiDAR inertial odometry는 LiDAR 센서와 IMU 센서를 사용한다는 것을 뜻한다.
  • Tightly-coupled는 센서 값들을 함께 인풋으로 받아 로봇의 자세와 지도를 추론하는 방법을 뜻한다. 반대의 의미로 센서들 각각 추론한 결과를 퓨전하는 loosely-coupled 방법이 있다 (자세한 설명을 원한다면 링크를 확인하면 좋다.).
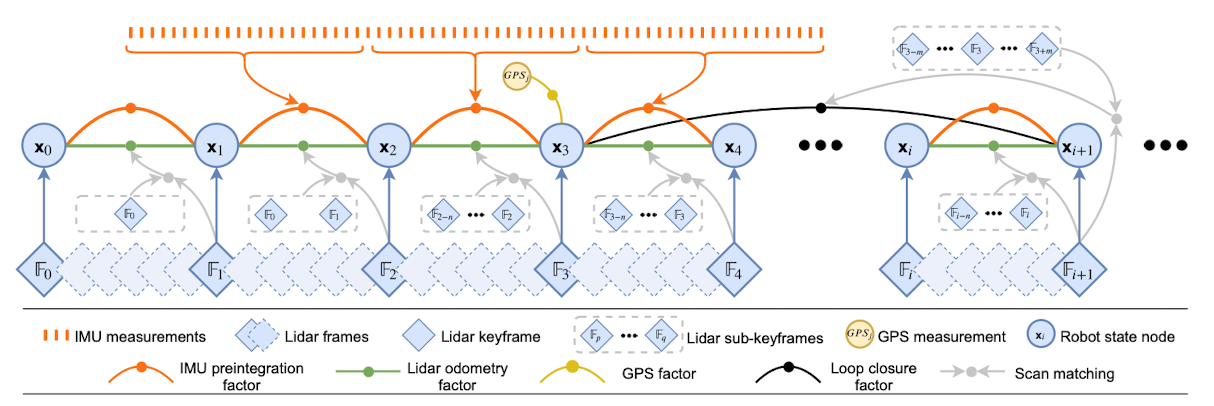
• Factor graph를 이용해 상대 이동치 (e.g. 라이다 scan matching, IMU kinematics)와 절대 위치 (e.g. GPS 신호)등의 정보를 조합할 수 있고, loop closure를 수행할 수 있다.
• LiDAR 스캔 도중에 움직이게 될 경우, 포인트가 밀려버리는 skew 문제가 생긴다. LIO-SAM에서는 LiDAR 스캔 도중의 움직임을 속도가 더 빠른 IMU 값을 받아 pre-integration함으로써 skew를 해결한다 (i.e. deskew).
• IMU pre-integration 값은 LiDAR odometry를 계산할 때 초기 값으로 사용되기도 한다.
• LiDAR odometry가 추론되면, 이 값을 이용해 IMU의 bias 값을 연산한다.
• 실시간 동작성을 유지하며 높은 정확도를 갖게 하기 위해, 포즈 최적화를 할 때에는 global map에 scan match를 하기보다는, 과거의 lidar scan을 marginalize한다.
  • Global map에 scan match를 하는 것 보다, local scale의 지도에 scan match를 하는게 훨씬 연산량이 적다. 효과적으로 local scale 지도를 만들기 위해 sliding window 방법으로 과거의 keyframe들을 이용하는데, 이를 sub-keyframe이라고 부른다.

 

---

Introduction

• 과거에 3D 공간을 라이다로 스캐닝하기 위해서 LOAM 기법을 자주 사용했다.
  • LOAM은 LiDAR와 IMU를 사용해 굉장히 높은 성능을 가졌지만, 몇가지 단점이 있었다.
    • 데이터를 global voxel map에 저장하는데, 이로 인해 loop closure detectiond이 잘 안되기도 하고, GPS와 같은 절대 위치 값을 이용한 자세 보정을 할 수 없었다. 또, feature가 많은 공간에서는 voxel map이 금방 꽉 차 연산속도가 느려지기도 했다.
• 이번 논문에서는 LIO-SAM을 소개한다.
  • 이하 abstract에서 소개한 LIO-SAM의 특징을 반복해서 다시 설명한다.

 

---

Related work

• LiDAR odometry는 주로 ICP 또는 GICP를 통해 구한다.
  • 포인트 클라우드 전부를 매칭하는건 연산량이 많아, 3D feature를 찾아 매칭하는 방법이 연구되었다. 주로 edge 또는 plane을 찾는 방법이다.
• LOAM
  • LiDAR scan 도중의 IMU pose를 구해서 LiDAR 포인트를 deskew한다.
  • 하지만 IMU 자체의 값이 pose 최적화에 들어가지는 않는다.
  • (그렇기 때문에 LOAM은 loosely coupled 방식이다)
• Lego-LOAM
  • Ground vehicle들에서 많이 쓰는 방법이다.
  • LOAM과 동일한 방법으로 IMU를 사용한다.
• EKF를 통해 LiDAR, IMU, GPS를 섞는 기법들도 있다.
• IMU를 최적화 수식에 섞을 때, 최신 기법들은 IMU pre-integration을 이용한다.
  • LINS는 error-state Kalman filter를 이용한다. 하지만 다른 absolute position 센서가 없기 때문에 (e.g. GPS) 오랜 시간동안 포즈 추정을 하다보면 drift가 커진다.
  • LIO-Mapping (LIOM)은 LiDAR와 IMU를 전부 최적화한다. 하지만 모든 프레임을 다 최적화해서 실시간 실행이 불가능하다. 저자가 테스트 했을 때는 실시간 속도의 60%만 나온다고 한다.

 

---

LIO-SAM

System Overview

• Frame 축 정리
  • World: W
  • Robot body frame B
    • IMU frame과 robot body frame이 동일하다고 가정한다. 그래야 수식을 적기가 쉽기 때문 ㅎㅎ
    • 혹시 자율주행처럼 자동차 frame과 IMU frame이 동일 위치에 설치되지 않을 경우, LIO-SAM을 수행하고 결과를 자동차 frame으로 옮겨주면 된다.
• Robot state x 정리
  • 3D 회전 (3x3 SO(3) 매트릭스) R
  • 3D 위치 p
  • 속도 v
  • IMU bias b
• Factor graph 정리
  • 4개의 factor
    • IMU pre-integration factor
    • LiDAR odometry factor
    • GPS factor
    • Loop closure factor
  • 1개의 variable - robot state x
    • 이동치가 특정 threshold가 넘을 때 마다 그래프에 추가된다.
  • 최적화 라이브러리로는 iSAM2를 사용한다.

 

---

IMU Preintegration error

가장 먼저 IMU의 기본 식부터 알아보자.

Equation (2)와 (3)은 각각 IMU 센서에서 얻을 수 있는 회전각속도 와 선형가속도 를 의미한다. 보통 회전각속도는 IMU 센서 내부의 gyro에서, 선형가속도는 linear accelerometer를 통해 얻는다.

Equation 2

$$\hat{\omega_t} = \omega_t + b^{\omega}_{t} + n^{\omega}_{t}$$

Equation (2)를 집중적으로 보자. 는 hat이 달려있다. hat 표시는 주로 ‘추정치’를 의미하는데, 센서가 추정한 값을 의미한다 (그냥 센서값이라고 보면 된다). 에는 hat이 없기 때문에 추정치가 아니므로 실제 물리공간에서 일어난 회전각속도를 의미한다. 는 Gyro bias이다. 는 gyro 센서 노이즈이다. 수식을 이해하자면, 실제 회전각속도 + gyro bias + gyro 노이즈 = gyro 센서 값 을 뜻한다.

Equation 3

$$\hat{a_t} = R^{BW}_t (a_t - g) + b^{a}_t + n^{a}_t$$

Equation (3)를 집중적으로 보자. 는 hat이 달려있으므로 선형가속도 센서 값이라고 이해하면 된다. 마찬가지로 는 실제 선형가속도 값이다. 는 중력방향으로의 가속도이다. 와 는 각각 accelerometer의 bias와 노이즈 값을 의미한다. IMU 값에는 중력가속도가 기본적으로 포함되어있기 때문에 (IMU 센서를 가만히 두면 중력가속도 값만 측정된다), IMU 값에서 중력값 만큼을 빼줘야 우리가 측정하고 싶은 움직임의 선형가속도를 구할 수 있다. 와 는 world frame 기준에서 측정된 값인데, 우리는 이 둘을 모두 robot body frame에서 연산하고 싶기 때문에 world->body frame으로 변환을 가능하게 하는 rotation matrix 를 곱해준다.

 

위 정보를 기반으로 velocity, position, rotation과 같은 시점에서의 로봇의 움직임을 구할 수 있다. 각각의 수식이 어떻게 나오는지 설명하기 전에, Wikipedia - kinematic equations 페이지 에서 ‘Kinematic equations for linear motion’을 같이 보면 좋다는 점을 미리 알린다.

Equation 4

$$\mathbf{v}_{t+\Delta t}=\mathbf{v}_{t}+\mathbf{g}\Delta t+\mathbf{R}_{t}(\mathbf{\hat{a}}_{t}-\mathbf{b}_{t}^{\mathrm{a}}-\mathbf{n}_{t}^{\mathrm{a}})\Delta t$$

우선 Equation (4) 부터 본다. 곧바로 보면 잘 이해가 가지 않을 수 있다. 이 수식이 어떻게 만들어지는지 보기 위해, velocity에 대한 기본적인 kinematic 수식에서부터 시작해보자.

$$v_{t+\Delta t} = v_t + a_t \Delta t$$

기본적인 velocity 수식은 다음과 같다. 에 를 곱하면 가속도 량 * 시간 량이니 속도 변화량이 나타난다. 이 값을 t 시점의 속도 값에 더해주면, 만큼의 시간이 지난 후의 속도 값을 알 수 있다.

우리는 velocity 식에서 요구하는 부분을 Equation 3에서 가져올 것이다. 하지만 는 우측 항에 있기 때문에, 식을 정리해줘야한다. 한줄 한줄 정리해보자.

$$\hat{a_t} = R^{BW}_t (a_t - g) + b^{a}_t + n^{a}_t$$ $$\hat{a_t} - b^{a}_t - n^{a}_t = R^{BW}_t (a_t - g)$$ $${R^{BW}_t}^{T} (\hat{a_t} - b^{a}_t - n^{a}_t) = {R^{BW}_t}^{T} R^{BW}_t (a_t - g)$$ $${R^{BW}_t}^{T} (\hat{a_t} - b^{a}_t - n^{a}_t) = a_t - g$$ $$a_t = g + {R^{BW}_t}^{T} (\hat{a_t} - b^{a}_t - n^{a}_t) = a_t$$

여기서, 는 적기 너무 어려우니, 라고 적는다. 논문에서 라고 적힌 부분이 이에 해당한다.

$$a_t = g + R_t (\hat{a_t} - b^{a}_t - n^{a}_t) = a_t$$

이제 를 velocity 수식에 대입한다.

$$\mathbf{v}_{t+\Delta t}=\mathbf{v}_{t}+ (\mathbf{g}+\mathbf{R}_{t}(\mathbf{\hat{a}}_{t}-\mathbf{b}_{t}^{\mathrm{a}}-\mathbf{n}_{t}^{\mathrm{a}}))\Delta t$$ $$\mathbf{v}_{t+\Delta t}=\mathbf{v}_{t}+\mathbf{g}\Delta t+\mathbf{R}_{t}(\mathbf{\hat{a}}_{t}-\mathbf{b}_{t}^{\mathrm{a}}-\mathbf{n}_{t}^{\mathrm{a}})\Delta t$$

Equation 4가 나왔다.

Equation 5

$$\mathbf{p}_{t+\Delta t}=\mathbf{p}_{t}+\mathbf{v}_{t}\Delta t+{\frac{1}{2}}\mathbf{g}\Delta t^{2} + \frac{1}{2}{\bf R}_{t}(\hat{\bf{a}}_{t}-{\bf{b}}_{t}^{\mathrm{a}}-{\bf{n}}_{t}^{\mathrm{a}})\Delta t^{2}$$

Equation 5도 곧바로 보면 잘 이해가 되지 않는다. Equation 4을 구할 때 얻은 정보를 이용하면 구할 수 있다.

Position에 대한 기본적인 kinematic 수식은 다음과 같다.

$$p_{t+\Delta t} = p_t + v_t\Delta t + \frac{1}{2} a_t \Delta t^2$$

우리가 아는 수식은 아래와 같다.

$$a_t = g + R_t (\hat{a_t} - b^{a}_t - n^{a}_t) = a_t$$

를 치환한다.

$$p_{t+\Delta t} = p_t + v_t\Delta t + \frac{1}{2} (g + R_t (\hat{a_t} - b^{a}_t - n^{a}_t)) \Delta t^2$$ $$p_{t+\Delta t} = p_t + v_t\Delta t + \frac{1}{2} g \Delta t^2 + \frac{1}{2} R_t (\hat{a_t} - b^{a}_t - n^{a}_t) \Delta t^2$$

Equation 5가 나왔다.

Equation 6

$$R_{t+\Delta t} = R_t \exp((\hat{\omega_t} - b^{\omega}_t - n^{\omega}_t)\Delta t)$$

Equation 6의 경우는 Lie theory에 대한 이해가 있어야한다. 쉽게 설명하자면, 3D 회전 값은 아주 작은 값에 대해서는 회전속도를 적분했을 경우 회전 값을 구할 수 있다. 즉, 는 찰나의 순간에서의 회전이기 때문에, 를 적분하면 된다는 것이다. 를 적분하면 linear space에서 연산이 되는데, 이는 Lie algebra의 영역에 있다. 이것을 exponential map을 통해 Lie group 영역으로 옮겨주면, 우리가 기존에 다루던 3x3 매트릭스 형태의 회전 매트릭스 형태가 된다. 회전 매트릭스 를 구하고 나면 기존의 에 더해야하는데, 회전의 누적은 덧셈연산이 아닌 곱셈연산으로 된다.

Equation 2에 에 대한 정보가 우측 항에 있다. 주 항이 되도록 수식을 정리해준다.

$$\hat{\omega_t} = \omega_t + b^{\omega}_{t} + n^{\omega}_{t}$$ $$\omega_t = \hat{\omega_t} - b^{\omega}_{t} - n^{\omega}_{t}$$

를 만들기위한 수식은 다음과 같다.

$$R_{\Delta t} = \exp (\omega_t \Delta t)$$

여기에 를 치환해준다.

$$R_{\Delta t} = \exp ((\hat{\omega_t} - b^{\omega}_{t} - n^{\omega}_{t}) \Delta t)$$

이것을 를 구하는 식에 치환한다.

$$R_{t+\Delta t} = R_t R_{\Delta t}$$ $$R_{t+\Delta t} = R_t \exp ((\hat{\omega_t} - b^{\omega}_{t} - n^{\omega}_{t}) \Delta t)$$

Equation 6가 만들어진다.

Equation 7,8,9

Equation 7,8,9는 유명한 IMU preintegration 논문에서 발췌한 수식을 그대로 사용한다. 이 수식을 통해 2개의 frame timestamp 사이의 velocity/position/rotation 변화를 추정할 수 있다. (언제 기회가 되면 이 논문도 리뷰해서 여기 설명할 예정이다.)

$$\Delta{\bf v}_{i j}=\mathrm{R}_{i}^{\mathsf{T}}({\bf v}_{j}-{\bf v}_{i}-\mathsf{g}\Delta t_{i j})$$ $$\Delta{\bf p}_{i j}=\mathrm{R}_{i}^{\mathsf{T}}({\bf p}_{j}-{\bf p}_{i}-{\bf v}_{i}\Delta a t_{i j}-\frac{1}{2}g\Delta t_{i j}^{2})$$ $$\Delta R_{i j}\,\ =\,R_{i}^{\textsf{T}}\,R_{j}$$

<계속 적는 중…>