비선형 최적화 Non-linear optimisation - Gradient descent, Newton-Raphson, Gauss-Newton, Levenberg-Marquardt

Posted on 2021-03-14 Edited on 2023-06-09 In 1. Spatial AI , 1.1 SLAM , 50가지 CV/SLAM 기술면접 질문들 Views:

모바일로 글을 보신다면 ‘데스크탑 버전으로 보기’를 누르시면 좀 더 보기 쉽습니다

예상 면접 질문

Gradient descent 방식, Newton-Raphson 방식, Gauss-Newton 방식, Levenberg-Marquardt 방식 최적화 기법은 어떻게 다른가요?

Gradient descent, Newton-Raphson, Gauss-Newton, Levenberg-Marquardt 최적화 방법들은 모두 continuous한 manifold위에서 optimal한 model parameter값을 찾기 위해 iterative하게 최적화하는 기법이다.
Iterative 하게 최적화하기 때문에 Initial value가 필요하다.
네가지 방법 모두 convex한 manifold 위에서 최적화 하는것을 전제로 두고 있다.
- 하지만 실제로 non-convex한 환경에 적용되었을 때 local minima에 빠질 수 있는데, 종종 특별한 테크닉을 사용하여 local minima에 빠지는 것을 방지하기도 한다. (e.g. Momentum)
SLAM에서 많이 쓰이는 방식은 Gauss-Newton, Levenberg-Marquardt 방식이다. 종종 Dogleg 방식을 쓰기도 한다.

Gradient descent방식은 딥러닝에서 많이 사용하는 기법으로써, manifold위 loss function을 최적화하기 위해 사용한다.
- Loss function은 L1 norm, L2 norm 및 다양한 norm을 사용할 수 있다.
- Initial point는 zero-initialization, random initalization, He initialization 등 여러가지 방법이 있다. (He init은 잘 모른다…)
작동 방식은 아래와 같다.
- 에서 시작하여, 우선 해당 위치의 derivative (i.e. Jacobian)을 구한다.
- 해당 Jacobian 매트릭스의 - 방향에 사전에 정의해둔 learning rate를 곱한 후, 에 더한다.
  - i.e.
  - 이를 통해, Manifold에서 에러가 작아지는 방향으로 움직일 수 있다.
단순히 Gradient descent 방식만 가지고는 처음 만나는 minima를 global minima라고 인식하게 된다.
- 즉, non-convex한 상황에는 local minima에 빠지기 쉽다.
- 이를 타파하기 위해 딥러닝에서는 momentum 등 다양한 기법들이 있다.

이미지 출처: KDnuggets Article By Keshav Dhandhania and Savan Visalpara.

Newton-Raphson 방식은 꽤 빠르게 해에 접근할 수 있는 방식이다.
작동 방식은 아래와 같다.
- 의 지점에서 1차 미분 값을 이용하여 접선 방정식을 만든다.
- 이 접선 방정식의 해를 로 삼는다.
- Converge 할 때 까지 루프.
Newton-Raphson 방식에는 치명적인 단점이 두개 있다.
- 첫째는, 2차 미분 값이 0이 되는 지점에서는 diverge 해버린다는 점.
- 둘째는, Local minimum이나 local maximum에서는 값이 진동 (i.e. oscillate)한다는 점이다.

이미지 출처: 네이버 블로그: 도마뱀님 - C언어)Newton-Raphson Method

SLAM에서 많이 사용하는 Gauss-Newton 방식으로 설명하겠습니다.
입력 데이터가 Gaussian 분포를 따르고 있다는 전제 하에, Least-squares 최적화 과정은 Maximum likelihood estimation으로 변환될 수 있다.
- 즉, 통계적으로 optimal한 해를 구할 수 있다.
한번에 Optimal한 해는 구하기 어려우며, 올바른 방향으로 iterative하게 최적화해야한다.
Non-linear한 manifold 위에서 최적화 방향을 잡기 위해 1차 미분을 수행한다. 1차 미분은 Taylor expansion으로 근사한다.
1차 미분 후 정리하면 2차 방정식 형태로 정리될 수 있다.
여기서 는 Hessian matrix로 근사된다.
2차 방정식은 미분한 결과가 0일 때, 최소값 또는 최대값을 얻을 수 있다. Convex인 형태이기 때문에 최소값을 얻을 수 있다.
를 푸는 방법에는 여러가지 방법이 있다.
- Parameter의 수가 많지 않으면 Inverse matrix를 구할 수 있다.
- Parameter의 수가 많다면, Cholesky decomposition이나 LU decomposition을 사용할 수 있다.
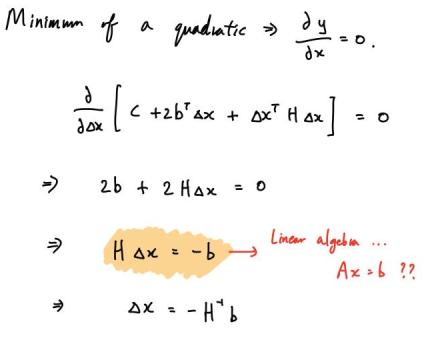
이러한 형태로 를 얻고나면, 을 얻을 수 있다.
- 이 후, iteration을 계속하면 된다.